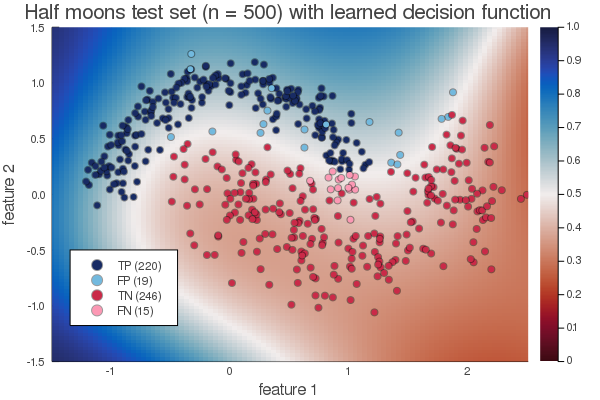
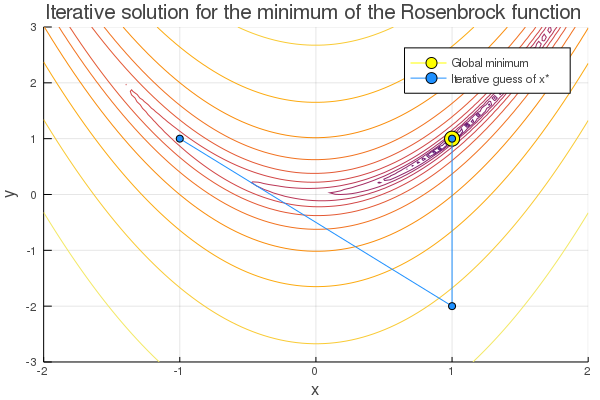
Google’s Tensorflow has seen great success in deep learning applications. How can we repurpose its functionality for mixed-integer optimization? Specifically, can we use its optimization capabilities to solve a sudoku?

Some plants grow better together, and some do not. Let’s optimize for it!

No GPU involved. It’s privacy-preserving, and uses parallel computing.

We use a sequence of regularization terms to force a decision variable in a convex problem to have an integer value. In this way, we can do Mixed Integer-Convex Nonlinear Programming (MICNLP) using convex optimization only, without using branch-and-bound methods.

I released the Julia package SequentialConvexRelaxation.jl, which applies a series of convex optimizations as a heuristic optimization method for nonconvex problems that can be described as convex problems with additional bilinear equality constraints. The software can be found here.

ZernikePolynomials.jl is a package for working with Zernike polynomials in Julia. I give a short introduction to the package. The software can be found here.

Sometimes the Sequential Convex Relaxation (SCR) approach to solving optimization problems with bilinear matrix equalities can suffer from slow convergence. Here we offer a strategy that can accelerate the convergence.

A sudoku puzzle is a nice example of integer programming where the goal is to find a solution that satisfies the rules of the game. We’re going to try and solve sudokus using convex optimization.

The travelling salesman problem is a mixed-integer programming problem where the objective is to find the best route past a selection of cities. Here we attempt to solve it in a non-traditional way: by using convex optimization.

Finding the optimal weights for a neural network is a non-convex optimization. However, is there a convex heuristic to find the optimal weights?