Mixed Integer-Convex Nonlinear Programming: forcing integrality by convex regularization

Introduction

The class of Convex Mixed-Integer Nonlinear Programming contains many important problems. One example is Operations Research, where one of the most common optimization problems is mixed Integer-Linear programming. For other examples, see for example (Bonami, Kilinç, & Linderoth, 2012).

In Nesterov’s “Lectures on Convex Optimization” Example 1.1.3 (Nesterov, 2018), he shows that the constraint that decision variables should be integer is a special case of nonlinear optimization by using the equivalent constraint

$$\sin ( \pi x) = 0.$$

This sine function crosses 0 if and only if $x$ is integer. When I first read this, I thought it was a rather peculiar (but correct!) way to deal with such a constraint, simply because I could not remember reading about anyone using this. Usually, researchers and practitioners resort to branch-and-bound or similar techniques to handle these integer constraints.

In earlier blog posts I used the bilinear constraint $x^2 = 1$ to encode binary constraints in optimization problems that fall into the “convex + binary variable” category. Even though we can use a conversion from bits to integers, by choosing the number of ‘bits’ (binary constraints) we still limit ourselves to an integer range.

In this post, we will develop a technique to iteratively ‘regularize’ a variable to an integer value, based on the sine constraint above. The approach can be summarized as follows:

• we approximate the constraint with a polynomial constraint based on an N-th order Taylor expansion of the function.
• we write the polynomial terms as a bilinear constraint on regular decision variables
• we use the Sequential Convex Relaxation approach to deal with the bilinear constraint
• we adjust the center of the Taylor expansion. We repeat the process several times until we (hopefully) find a feasible solution of the original problem with a good performance.

Taylor expansions and approximations

The function $f(x) = \sin(x)$ has a $N$-th order approximation from its Taylor series expansion around $a$:

$$f(x) \approx \sum_{n=0}^N \frac{f^{(n)}(a)}{n!}(x-a)^n$$

We introduce the following notation for the coefficients

$$c_n^a = \frac{f^{(n)}(a)}{n!},$$

giving the expansion

$$f(x) \approx c_0^a + c_1^a (x-a)^1 + \ldots + c_N^a (x-a)^N.$$

Alternatively, with

$$z_n = (x-a)^n$$

we have

$$f(x) \approx c_0^a + c_1^a z_1 + \ldots + c_N^a z_N$$

Polynomial terms as bilinear constraints

Among the variables $z_n$ we have the relation $z_n = z_1 z_{n-1}$, or in matrix form

$$z_1 \begin{bmatrix} z_1 & \cdots & z_{N-1} \end{bmatrix} = \begin{bmatrix} z_2 & \cdots & z_{N} \end{bmatrix}.$$

This is in the form $APB = C$ with $A,B,C$ decision variables and $P$ a constant parameter. Here, the appropriate values are

$$A = z_1, ~ P=1, ~ B=\begin{bmatrix} z_1 & \cdots & z_{N-1} \end{bmatrix}$$

and

$$C = \begin{bmatrix} z_2 & \cdots & z_{N} \end{bmatrix}.$$

Apart from the bilinear constraint to enforce the polynomial structure, we need to enforce

$$0 = f(z) \approx \tilde{f}_a(x) = c_0^a + c_1^a z_1 + \ldots + c_N^a z_N$$

with $a$ sufficiently close to the integer and $N$ large enough. We do this by using the norm of $\tilde{f}_a(x)$ in the objective term.

Using Sequential Convex Relaxation to enforce the polynomial constraint

To find an integer using convex optimization, we use the convex relaxation technique of (Doelman & Verhaegen, 2016) with a twist. The basis is the following optimization problem:

$$\begin{equation*} \begin{aligned} & \text{minimize} && \| \tilde{f}_a(x) \|_2 + \|M(A,P,B,C,X,Y)\|_*, \\ \end{aligned} \end{equation*}$$

where we have used the affine (in $A,B,C$) matrix structured function $M$ identical to that of previous posts and that in (Doelman & Verhaegen, 2016) $X,Y$ as described below. This structure is as follows:

$$M(A,P,B,C,X,Y) = \begin{bmatrix}C + APY + XPB + XPY & (A+X)P \\ P(B+Y) & P \end{bmatrix}.$$

If the rank of $M$ equals 1, we have the condition that $APB=C$, and the desired polynomial relation between the variables $z_n$. As a convex relaxation of the rank constraint, we use the nuclear norm of $M$ in the objective function.

So to summarize the objective function, the first term stimulates finding a solution where $sin(x) = 0$ (the original problem is $\sin(\pi x)$ but this differs by only a scaling of the decision variable) and the second one tries to enforce the polynomial structure.

We iteratively solve this (convex!) problem, but each time we can change the values for $X,Y$ and the coefficients $c_n^a$. Or even the order of the Taylor approximation.

Usually we have a very simple update for $X,Y$, where we use the optimal values for $A$ and $B$:

$$X = -A^*,~ Y = -B^*$$

However, we can do something else. For example

$$Y = - \begin{bmatrix} z_1 & \cdots & z_1^{N-1} \end{bmatrix}$$

or use the optimal $x$ for our new $a$ (of the Taylor expansion) giving

$$Y = - \begin{bmatrix} z_{a,1} & \cdots & z_{a,1}^{N-1} \end{bmatrix}$$

which should be all 0. We can even mix these to see what gives the best result.

Numerical tests

I implemented the relaxation scheme for $f(x) = \sin(\pi x)$ with 4 updates of the Taylor expansion point, each of these after 3 default iterations of the Sequential Convex Relaxation scheme. Running the initial ‘guesses’ for the variable between -5 and 5, I obtained the following beginning end ending variables:

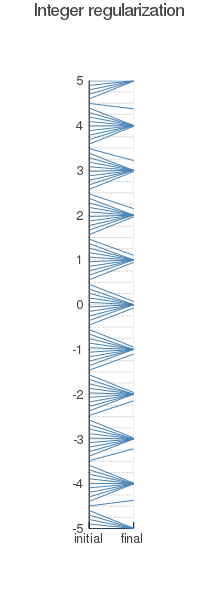
Here the value of the variable at the start is connected by a straight line to the value at the end.

As can be seen, the variables get regularized to integer values, but every $.5$ in a starting variable seems to give some difficulties.

Conclusion

I demonstrated how a sequence of convex optimizations can lead to integer-valued decision variables, without using branch-and-bound or similar techniques. This opens up the investigation of solution techniques for mixed Integer-Convex optimization problems that do not have the exponential growth of computational complexity from which current branch-and-bound techniques suffer.

The performance of this relaxation scheme on (large scale) mixed Integer-Convex optimization problems, and the required tuning rules, is something we will investigate in the future.

Furthermore, using Taylor approximations (in a single variable or even multiple) in an iterative manner as we did here for the function $f(x) = sin(x)$, allows us to investigate many more functions with Taylor approximations that can be added as constraints to problems that were originally convex, but with the addition of the functional constraint become non-convex.

Bibliography

1. Bonami, P., Kilinç, M., & Linderoth, J. (2012). Algorithms and software for convex mixed integer nonlinear programs. In Mixed integer nonlinear programming (pp. 1–39). Springer.
2. Nesterov, Y. (2018). Lectures on convex optimization (Vol. 137). Springer.
3. Doelman, R., & Verhaegen, M. (2016). Sequential convex relaxation for convex optimization with bilinear matrix equalities. In 2016 European Control Conference (ECC) (pp. 1946–1951). IEEE.