Speeding up Sequential Convex Relaxation: Random Rescaling

Introduction

The Sequential Convex Relaxation (SCR) method is an algorithm that provides a heuristic method for solving optimization problems that have bilinear constraints on decision variables.

The class of problems is NP-hard, and global optimality cannot always be verified. However, the method does not need to be supplied with a feasible solution to start, which is an important difference with many other techniques. For many problems the method gives satisfactory results.

Depending on the problem, the convergence can be slow. For example, see the following figure, where the constraint violation is plotted for a simple matrix factorization problem.

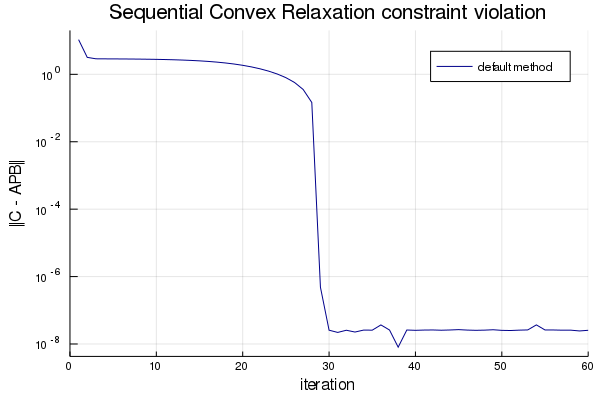
The method converges in 30 iterations, but depending on the problem, it may be many more before the algorithm reaches the convergence “cliff”. In this article we propose an incredibly simple heuristic method, an adjustment to the original algorithm that often shows great improvements in performance.

Standard Sequential Convex Relaxation

The standard SCR method works as follows. Assume we are given an optimization problem as follows:

$$\begin{equation} \begin{aligned} & \text{minimize}_{x,A,B,C} && f(x,A,B,C) \\ & \text{subject to} && C = A P B \end{aligned} \end{equation}$$

with decision variables $x$, a vector, and $A,B$ and $C$, which are matrix-valued decision variables. In the constraint the matrix $P$ is not a decision variable but a known, fixed matrix-valued parameter that is specified by the problem.

The following constraint is equivalent to the constraint $C=APB$ for any invertible parameter matrices $W_1,W_2$ and any parameter matrices $X$ and $Y$ of appropriate size (i.e. size of $A$ and $B$ respectively):

$$\text{rank}~M(A,P,B,C,X,Y,W_1,W_2) = \text{rank}~P$$

where the matrix-valued function $M$ is of the form

$$\begin{bmatrix} W_1 (C + APY + XPB + XPY) W_2 & W_1(A+X)P \\ P(B+Y)W_2 & P\end{bmatrix}$$

The iterative SCR method solves the following problem for iteration $k$:

$${A_{k},B_{k}} = \text{arg min} f(x,A,B,C) + \lambda || M(A,P,B,C,-A_{k-1},-B_{k-1},W_1,W_2) ||_*$$

where $W_1$ and $W_2$ are usually identity matrices. $|| \cdot ||_*$ denotes the (convex) nuclear norm, the sum of the singular values of the (matrix-valued) argument. $\lambda$ is a regularization parameter.

The resulting problems are convex, even though the original problem is generally not. The regularization term stimulates finding feasible solutions of the underlying NP-hard optimization problem.

Random Reweighting

The figure above shows the constraint violation for a simple matrix factorization problem where $C$ and $P$ are given:

$$\begin{equation} \begin{aligned} & \text{find}~ A,B~ \text{subject to}~ C = A P B \end{aligned} \end{equation}$$

We see very little change between iteration 2 and 20. We attribute this to a bad scaling of the problem. Our suggested solution is to rescale the problem randomly. That is, at each iteration we generate a $W_{1,k}$ and $W_{2,k}$ with elements drawn randomly from a Gaussian distribution or a uniform distribution between -1/2 and 1/2. Then we scale the matrices to have maximum singular values equal to 1. These particular choices of random distributions have the property that, on average, the singular values show the same linear declining trend with increasing singular value number.

The result can be spectacular, see the following figure:

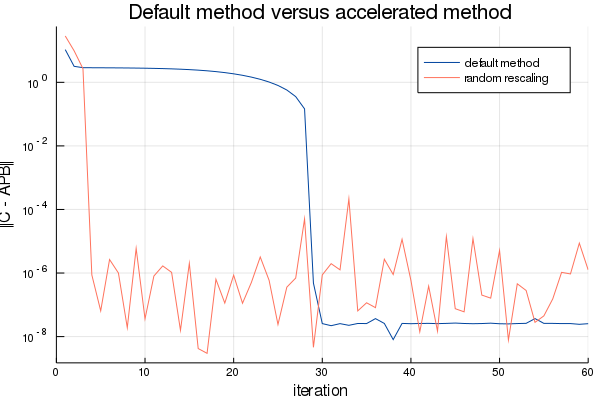
The convergence here is much faster!

A numerical simulation

The next question to ask is: to what degree is the fast convergence a random occurrence?

We ran the same problem 300 times, and below you see a histogram showing the number of times the algorithm converged after a specific number of iterations:

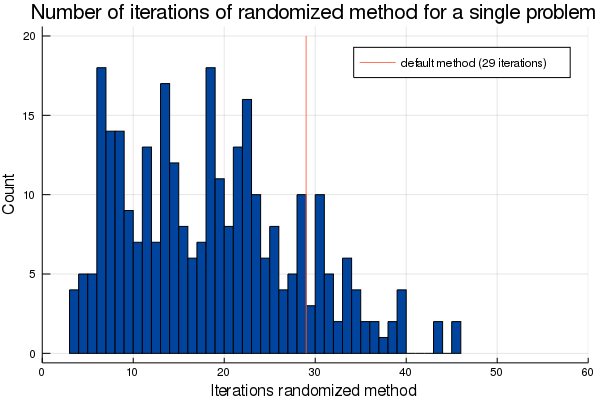
In 85% of cases we have faster convergence!

Does it depend on this specific problem? Yes. Sometimes the standard method converges quickly, sometimes it doesn’t. So below you see an experiment where each time a random matrix factorization problem was generated (different low rank $C$, different $P$) and both versions of the algorithm were run. The dots indicate how many iterations the default algorithm took (horizontal axis) versus the amount the randomly reweighted algorithm took (vertical axis). The number of iterations was limited to 50.

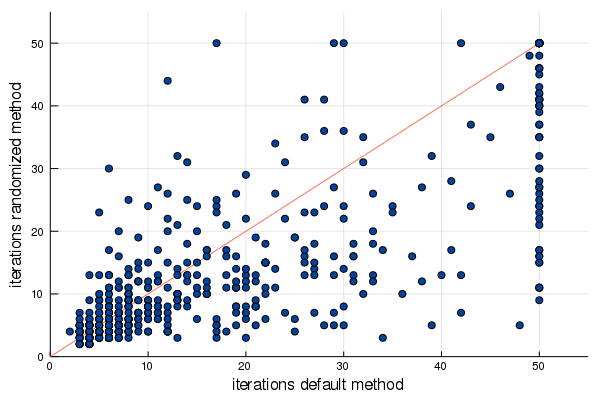
From this figure we draw two conclusions: If the default method was fast to converge, the randomly reweighted method was fast too, and usually a little faster. If the default method was not fast to converge, the randomly reweighted method was very often much faster to converge!

Conclusion

We introduced a method to improve the convergence speed of the Sequential Convex Relaxation algorithm. The weights are randomly adjusted every iteration, so that the problem is a differently scaled convex heuristic for the same original NP-hard problem. Slow convergence due to ‘flat valleys’ in the objective function are then often overcome by making them “steep” by chance. Further research is needed to find systematic ways to choose these weights to always have better convergence than the default method.