Optimal square foot gardening with companion planting and mixed-integer programming

Optimal square foot gardening with companion planting and mixed-integer programming

If you are planning next year’s vegetable or herb garden, one way to do that is to use the square grid layout in what is called square foot gardening. The principle is simple: divide your plot in a square grid, and assign to each square a specific plant. For example: square 1 will have beets, square two carrots, and so on.

There is also something called companion planting: the growing of plants in close proximity to both their benefit. A well known example is squash, maize and beans being grown together for thousands of years in Mesoamerica.

Let’s combine these two concepts into optimal square foot gardening: planning the vegetable garden in such a way that plants grown next to each other, stimulate each other, and those that negatively effect each other are spaced apart.

I’ll formulate this into a mixed binary-linear programming problem, allowing us to give up requirements on the number and type of vegetables we want in the garden, and letting a solver figure out where to best put them.

The optimization problem

The garden is assumed to be rectangular with a grid of size $n_i \times n_j$, and that we have to pick from $n_k$ vegetables. Let’s introduce the decision variables $x_{i,j,k} \in \{0,1\}$ to indicate whether vegetable $k$ is grown in square $i,j$.

To ensure the garden is full, we have the constraint

$$\sum_k x_{i,j,k} = 1 \quad \forall i,j.$$

Because we need keep track of which vegetables grow next to each other, we use a variable $w_{i_1,j_1,k_1,i_2,j_2,k_2}$, where

$$w_{i_1,j_1,k_1,i_2,j_2,k_2} = \begin{cases} 1 & \text{if}~x_{i_1,j_1,k_1} = x_{i_2,j_2,k_2} = 1,~(i_1,j_1)~\text{next to}~(i_2,j_2) \\ 0 & \text{otherwise}\end{cases}$$

We can code this using

$$\begin{aligned} & w_{i_1,j_1,k_1,i_2,j_2,k_2} \in [0,1] \\ & w_{i_1,j_1,k_1,i_2,j_2,k_2} \leq x_{i_1,j_1,k_1} \\ & w_{i_1,j_1,k_1,i_2,j_2,k_2} \leq x_{i_2,j_2,k_2} \\ & w_{i_1,j_1,k_1,i_2,j_2,k_2} \geq x_{i_1,j_1,k_1} + x_{i_2,j_2,k_2} -1 \end{aligned}$$

if $(i_1,j_1)$ is next to $(i_2,j_2)$ (and for simplicity we’re only counting top, bottom, left and right, no diagonals), and 0 if they are not.

Any constraints on the minimum number of vegetables of a specific type, $r_k$, can be encoded using

$$\sum_{i,j} x_{i,j,k} \geq r_k \quad \forall k$$

Now, for the objective. Assume we have some symmetric matrix $B$ where $B_{k_1,k_2}$ is positive if plants $k_1$ and $k_2$ stimulate each other and negative if they do not. The actual values can maybe be estimated from data, but for simplicity purposes I’m using simple rules with $B_{k_1,k_2} \in \{-2,-1,0,1,2\}$ according to a table I found:

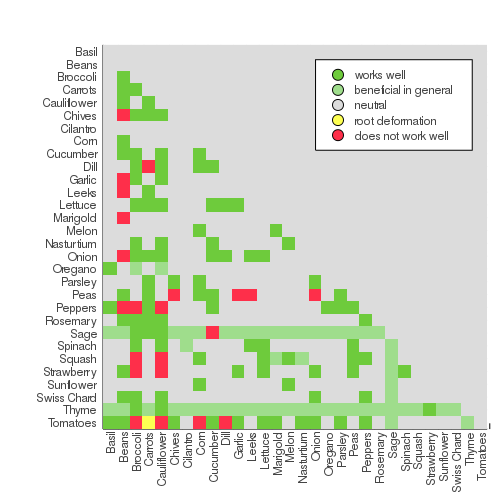
The objective is to sum up the bonusses (or negative scores) for each pair of squares:

$$\sum_{i_1,j_1,k_1,i_2,j_2,k_2} w_{i_1,j_1,k_1,i_2,j_2,k_2} B_{k_1,k_2}$$

This problem is a mixed Binary-Linear programming non-convex optimization problem, that we can try to solve with for example Julia, JuMP and the Cbc solver.

Example

Let’s say we try to plant a vegetable garden that is 4 by 6 squares, and plant it with at least 3 of each of the following vegetables:

• Beans
• Corn
• Peas
• Peppers
• Squash
• Tomatoes

and we have the following scoring matrix:

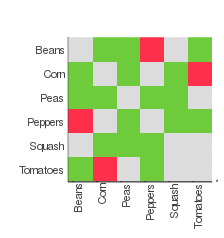
Running the optimization with a timeout of 90 seconds, we get back the following plan:

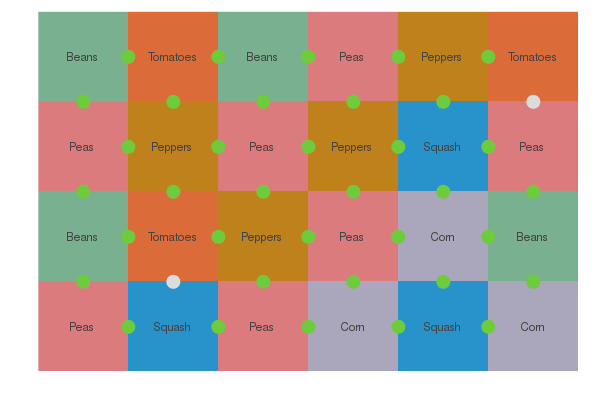
I indicated the different vegetables by color, and the score is indicated by a colored circle. I’d say this is a pretty good solution! Only two edges are not giving a positive boost, and none have negative effects.

Conclusion

I described a way to optimize the layout of a vegetable garden.

The optimization technique will need further research. The optimization problem as stated here gets really large really quickly with increasing size of grids and possible vegetables. Perhaps the convex relaxation technique I’ve used in other posts can handle these, because this large scale MBLP will turn into a series of large LPs. Even though this not necessarily gives the optimal solution, maybe we will obtain a very good one anyway. Another possible technique avoids having so many variables is a Genetic Algorithm, so maybe that’s the path forward.

Maybe the future of this technique is not so much in small vegetable gardens, but in larger farms that want to grow multiple crops in a way that minimizes large contiguous fields of monocrops. Before we’re there though, I assume research is necessary to make actually farming such a diverse field economically viable and technically possible. Different crops need different attention.